I. 문제의 정의 및 계획

전체적인 방향이 결정되는 가장 중요한 단계로 다음의 절차가 필요하다.

1. 대상 제품 혹은 시스템의 구조와 원리 파악

CFD는 물리적 현상을 모사하는 것이기 때문에 대상의 물리 현상에 대한 이해가 필수적이다.

2. 해석의 목적과 해석을 통해 얻고자 하는 결과는 무엇인지 정리

해석의 목적과 결과가 불분명 할수록 불필요한 많은 물리 모델이 포함되고 모델링도 복잡해져 계산 비용이 크게 증가할 수 있다. 목적에 맞게 해석 모델을 최대한 단순화하는 것이 중요하다.

3. CFD 계산의 타당성 검토(지배방정식 검토)

유체의 흐름의 지배방정식인 Navier-Stokes 방정식은 유체가 연속체라는 가정을 사용하고 있기 때문에, 이 가정이 대상 문제에서 타당한지를 확인한다. 대부분의 유체는 연속체 가정이 타당하지만 진공도가 매우 낮을 때는 연속체 가정의 타당성 검토가 필요하다.

* 진공도에 대한 평가 방법 자세히 보기

유체역학에서 진공은 대기압보다 낮은 압력인 상태를 뜻한다. 우주 공간이나 반도체 제조 공정 등에서 연속체 가정을 사용할 수 없는 조건이 있다. 연속체 가정은 유동의 특성 길이가 분자의 평균 자유 경로(mean free path)보다 매우 클 때 성립한다.  분자의 평균 자유 경로와 유체의 특성 길이의 비율을 Knudsen number, $Kn$ 라고 하며 다음과 같이 정의된다.

$K_n = \frac{\lambda}{L} = \frac{k_B T}{\sqrt{2} \pi {\sigma}^2p L} = \frac{Ma}{Re} \sqrt{\frac{\gamma \pi}{2}}$

$\lambda$ : 분자의 평균자유경로(mean free path)
$L$ : 유체의 특성길이(characteristic length)
$k_B$ : 볼츠만 상수(Boltzmann’s constant, 1.38e-23 J/K)
$\sigma$  : 유체 분자의 직경
$\gamma$ : 비열비(ratio of specific heat)

Knudsen number 가 0.01 이하이면 연속체 가정을 사용할 수 있어 Navier-Stokes 방정식을 사용할 수 있다.

0.01 이상의 영역을 희박 기체(rarefied gas)라고 한다. 0.01~0.1 범위이면 slip flow 영역, 0.1~10 범위이면 transition flow, 10 이상이면 free molecular flow 영역이다. Knudsen number가 0.01~1인 영역에서는 DSMC(Direct Simulation Monte Carlo) 방법을 사용할 수 있다. DSMC는 Navier-Stokes 방정식이 아닌 Boltzmann 방정식을 사용하며 OpenFOAM은 DSMCFoam 이라는 솔버를 제공한다. Knudsen number가 1보다 큰 경우 분자동역학(molecular dynamics)을 이용하여 계산해야 하며 전산유체역학에서 다루는 영역은 아니다.

4. 목표로 하는 결과의 정확도를 명확히 한다

• 대상 문제와 유사한 논문이나 기술 자료들을 탐색한다.
• 정량적으로 정확한 결과를 얻기 위한 시뮬레이션이라면 목표로 하는 정확도의 수준을 결정한다. 정확도를 평가의 근거 확보를 위해 논문이나 계측 결과를 찾는다.
• 정성적 특성을 파악하는 것이 목표인 경우 다양한 조건의 결과가 일관적인 경향을 나타내는지 확인할 수 있는 방법론을 마련한다.

5. 해석할 경우의 수를 결정한다

• 해석해야 할 형상 및 조건에 따라 케이스의 종류를 결정한다.
• 많은 해석 케이스가 필요한 경우 자동화 전략을 수립한다.

6. 일정을 확인한다

• 하드웨어 리소스를 고려하여 전체 일정에 문제가 없는지 확인한다.
• 단계별 우선 순위를 고려하여 전체 일정을 수립한다.

II. 격자 생성 과정

계산을 위한 격자 생성은 다음과 같은 과정으로 이루어 진다.

1. 형상 준비

계산 영역을 결정하고 형상 단순화 수준을 결정한 후 CAD 파일을 수정한다.

1.1 계산 영역의 결정

내부 유동의 경우 계산 영역은 확실한 경계조건을 줄 수 있는 영역까지 잡아야 한다. 외부 유동일 때 원방 경계 영역은 baramMesh에서 육면체를 이용해 만든다. 형상의 대칭성과 주기성을 고려하여 절반 혹은 일부만 모델링 할 수 있는지 결정한다. 격자 수를 절반 이하로 줄일 수도 있기 때문에 명확히 결정해야 한다.

1.2 형상 단순화 수준 결정

유동에 큰 영향을 미치지 않는 부분을 삭제하고, 복잡한 형상을 cell zone 모델로 대체할 수 있는지, 얇은 두께의 고체를 두께가 없는 baffle로 처리할 수 있는지 결정한다.

경계면과 cell zone, interface 구성 방법을 결정한다. 경계면을 구성할 때 후처리 항목을 고려해야 한다. Cell zone 모델을 사용할 영역을 결정한다. 형상의 주기성과 baffle을 고려하여 interface를 결정한다.

1.3 Multi-region 여부 결정

고체의 전도가 포함되어 있을 때 고체를 경계조건으로 처리하는 방법과, 유체와 고체 영역을 따로 모델링해서 다중 영역(multi-region)으로 계산하는 두 가지 방법이 있다. 고체 두께 방향의 1차원 열전도만을 고려해도 될 때는 고체 영역을 따로 모델링하지 않고 1차원 열전도를 포함하는 경계조건으로 처리할 수 있다. 고체의 두께 방향 뿐 아니라 다른 방향의 열전도를 함께 고려해야 하거나, 비정상상태 문제인 경우는 다중 영역으로 계산해야 한다.

문제에 맞게 고체 영역 형상을 어떻게 처리할 것인지를 결정한다.

1.4 CAD Clean up

CAD 파일에서 불필요한 영역을 제거하고 찢어지거나 연결되어 있지 않은 부분을 정리한다. 경계면으로 나누어져야 되는 부분을 분리한다.

2. baramMesh의 실행 및 형상 설정(Geometry)

baramMesh를 실행하고 형상 파일을 불러온 후 배경 격자, 격자 분할(mesh refinement), cell zone을 위한 영역을 만든다.

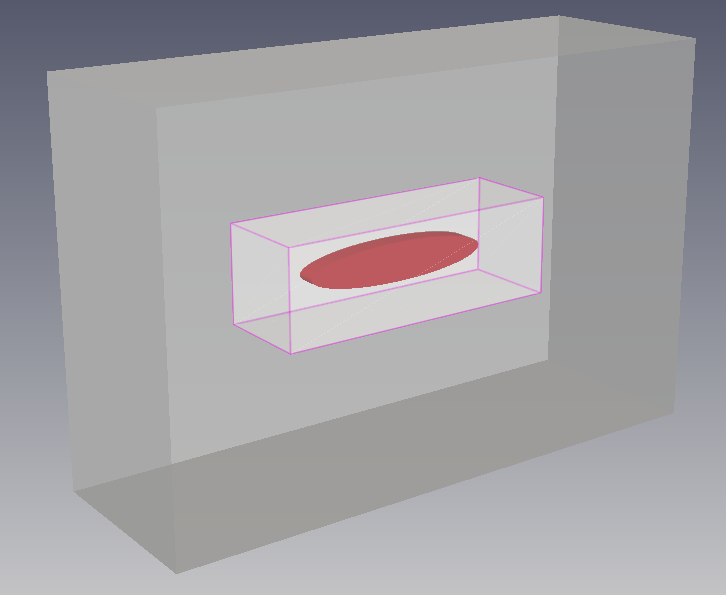
2.1 형상 파일 불러오기

현재 baramMesh에서는 STL(STereoLithography) 파일을 이용한다. 형상 파일을 불러 올 때 경계면 분리를 위해 feature angle을 이용해 면을 나눌 수 있다.

2.2 원방 경계 영역 만들기

외부 유동일 때 원방 경계면이 될 전체 영역을 생성한다. 육면체의 6개 면이 나누어지는 Hex6를 이용한다. 내부 유동일 때는 따로 만들 필요는 없다.

원방 경계의 크기는 유동의 압축성 여부에 따라 달라진다. 비압축성 유동의 경우 일반적으로 입구 방향으로 물체 길이의 3~5배, 출구 방향으로 10~15배, 측면과 상하 방향은 5~10배 정도를 사용한다. 초음속 유동의 경우 후류의 정보가 상류로 전달되지 않기 때문에 입구 방향으로 1~3배, 출구 방향으로 5~10배 정도로 작게 잡을 수 있다.

2.3 격자 분할 영역 만들기

격자의 기본 크기, 격자 조밀도의 분포, 형상의 곡률과 간격(gap) 등을 고려하여 전체적인 격자 구조를 결정한다. 격자 크기의 결정은 유동의 변화를 모사할 수 있는지가 중요하며 이와 함께 작은 형상을 정확히 구현할 수 있는지도 고려해야 한다. 이에 따라 격자 크기 조절을 위한 격자 분할 영역(refinement zone)을 생성한다.

육면체, 실린더, 구 등을 이용해서 형상을 만든다. 격자 분할을 위한 영역의 면(surface)들은 속성을 None으로 지정해 주어 경계면이 아님을 설정해야 한다.

2.4 Cell zone 영역 만들기

Porous, MRF, Sliding mesh, 소스 항 등의 설정을 위한 영역을 육면체, 실린더, 구 등을 이용해서 만든다. cell zone의 면들이 경계면이 아님을 지정해 주어야 하며, sliding mesh, multi-region 등을 위한 면은 interface로 설정해 주어야 한다.

3. Region 설정

• Single region 문제인 경우 형상의 외부에 격자를 만들지 혹은 내부에 격자를 만들지를 지정한다.
• Multi-region 의 경우 region 별로 격자를 만들 영역을 지정한다.

4. 배경 격자(Base Grid) 생성

blockMesh 유틸리티를 이용해서 육면체 배경 격자를 생성한다. x, y, z 방향의 개수에 따라 육면체의 크기와 모양이 결정된다.

5. 격자 분할(castellation)

배경 격자를 분할하고 불필요한 영역의 격자를 제거하는 단계이다.

• Feature line, surface, volume의 격자 레벨을 설정한다.
• 면(Surface)의 곡률에 따른 자동 분할(curvature refinement) 옵션을 사용할지 설정한다.
• 체적(volume)에서 간격에 따른 자동 분할(gap refinement) 옵션을 사용할지 설정한다.

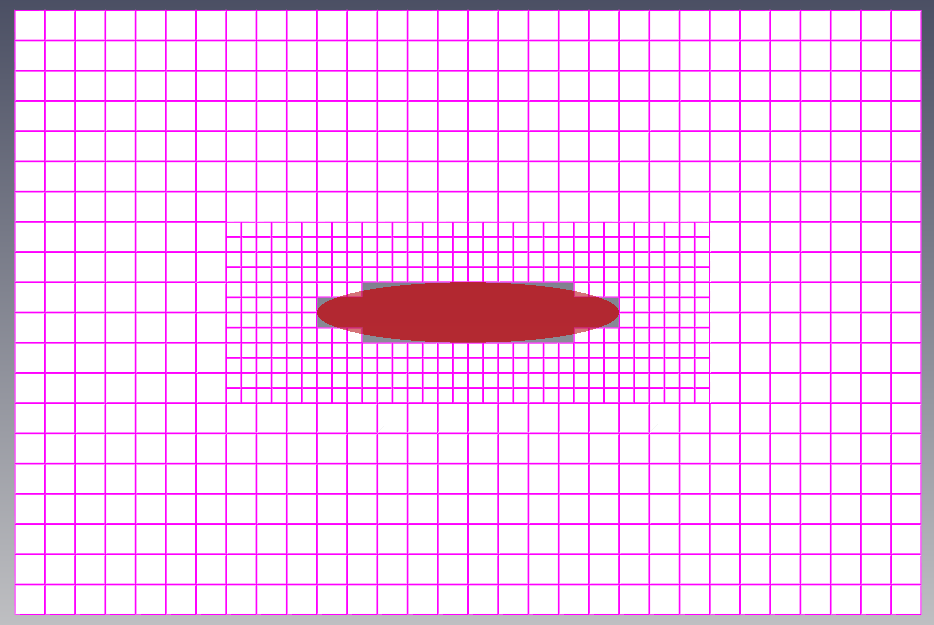
6. 형상 구현(snap)

격자점을 물체 표면으로 이동시켜 형상을 구현하는 단계이다.

• Implicit와 explicit 방법을 선택한다. Explicit은 stl 파일을 읽을 때 자동으로 만들어지는 feature line을 이용하는 것이고, implicit은 feature angle을 이용해서 직접 찾는 방법이다. 형상을 구성하는 면들이 교차되는 곳이 분리(split)되어 있지 않을 때 그곳에 feature line이 생성되지 않기 때문에 implicit 방법을 추천한다.
• 격자의 품질을 유지하기 위한 smoothing, relaxation 관련 여러가지 변수들을 설정한다
• 경계면 및 cell zone 경계에 buffer layer를 생성할지 설정한다.

7. 경계층 격자 생성

• 경계층 격자를 만들 경계면을 선택한다. 모든 벽면에 경계층 격자를 만들 필요는 없으며 속도가 0인 벽면들 중 경계층 유동이 중요한 것들만 선택한다.
• 경계층 격자의 두께, 개수, 두께 증가 비율을 결정한다.
• 격자 품질 유지를 위한 여러가지 옵션을 설정한다.

* 벽함수(Wall function)와 y+ 자세히 보기

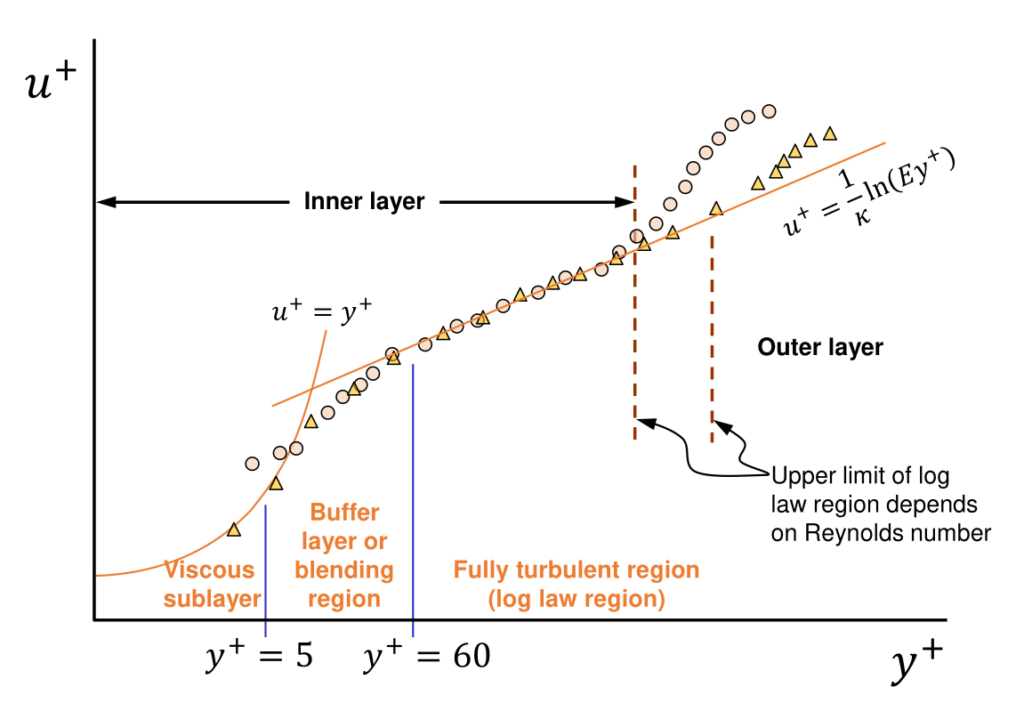
속도가 0인 벽면 근처에서는 급격한 속도 구배가 있다. 무차원화된 벽으로부터 거리인 y+ 값이 5 이하인 점성저층(viscous sublayer)의 속도 기울기는 선형이다. y+ 값이 30~300인 대수영역(log layer)의 속도 기울기는 로그 함수로 나타낼 수 있다. y+ 값 5~30 구간은 완충영역(buffer layer)이다. 이 속도 분포를 이용하여 벽면으로부터 첫번째 격자의 속도를 결정하는 방법이 벽함수(wall function)이다.

k-epsilon, SST k-omega 모델을 사용할 때 y+는 30~100 정도의 범위에 있도록 첫번째 경계층 격자의 높이를 사용하는 것이 좋다.

y+는 다음의 식으로 계산되는데 속도의 함수이기 때문에 정확한 값은 CFD 해석이 끝나야 알 수 있다. 격자 생성 단계에서는 특성 속도를 이용하여 대략적인 높이를 결정할 수 있다.

$y+ = \frac{y U*}{\nu}$

$U* = \sqrt{\frac{\tau_w}{\rho}}$

$\tau_w = C_f \cdot \frac{1}{2} \rho U^2$

$C_f = [2 log_{10} (Re_x ) – 0.65]^{-2.3}$

$U*$ : friction velocity

8. 내보내기

baramFlow에서 읽을 수 있는 격자 폴더를 생성한다. 특정 면을 이용해서 2차원 격자 혹은 축대칭 격자로 내보낼 수 있다.

III. 해석 실행 과정

1. 솔버 설정 – 압축성 유동, 다상유동

• baramFlow를 실행
• 압력 기반 솔버인지 밀도 기반 솔버인지 선택
• 압력 기반 솔버이면 다상유동인지 선택

1.1 압력 vs 밀도 기반 솔버 – 압축성 유동

유동의 속도가 음속에 가깝거나 더 큰 경우 충격파를 잘 포착할 수 있는 밀도 기반 압축성 솔버를 사용하는 것이 효과적이다.

* 압축성 유동 판단 자세히 보기

마하수(Mach No.)를 이용해 압축성 유동인지를 판단한다. 넓은 의미의 압축성 유동은 밀도가 일정하지 않은 유동을 말한다. 온도 차이에 의해 밀도가 변하는 경우도 이에 포함된다. 하지만 여기서는 좁은 의미로 유동의 속도에 의해 밀도가 변하는 것을 의미한다.

$M = \frac{U}{a} = \frac{U}{\gamma R T}$

$\gamma$ : 비열비
$a$ : 음속
$R$ : 기체상수

마하수 0.3까지는 비압축성유동, 0.3~0.8 영역을 아음속, 0.8~1.2 영역을 천음속, 1.2 이상을 초음속, 5 이상을 극초음속이라 한다. 보통 아음속 영역에서는 충격파가 없으며 비압축성 유동을 계산하는 압력기반 솔버로도 해석이 가능하다. 천음속 영역부터는 충격파를 포착할 수 있는 기법이 포함된 압축성 솔버를 사용해야 한다.

밀도 기반 솔버는 정상상태는 TSLAeroFoam, 비정상상태는 UTSLAeroFoam 솔버가 사용된다.

1.2 다상 유동

시스템에 두 가지 이상의 상(phase)이 있을 때 각 상을 포함하는 다상 유동으로 계산할지 주요한 하나의 상에 대해서만 계산할지 결정한다.

현재 Baram은 상들의 경계면이 명확히 분리된 모델인 VOF(Volume Of Fluid)와 캐비테이션 모델을 지원한다.(각 상들 마다 별도의 운동량방정식을 계산하는 Eulerian 모델과 입자의 운동을 Lagrangian 방식으로 계산하는 DPM(Discrete Phase Model)은 아직 지원하지 않는다.)

다상 유동에는 interFoam, multiphaseInterFoam, interPhaseChangeFoam 솔버가 사용된다.

2. 격자 불러오기, 격자 단위와 품질 확인

• File – Load Mesh 메뉴에서 격자를 불러온다.
• Mesh – Info 메뉴에서 격자를 확인한다.
  • baramMesh는 단위가 없는 반면 baramFlow은 미터 단위를 사용한다. 격자의 크기를 확인하고 단위가 제대로 되어 있는지 확인한다. 필요 시 Mesh-Scale 메뉴에서 단위를 맞춰준다.
  • 격자의 최소 체적이 음수가 아닌지 확인한다.
  • 그래픽 상에서 격자에 문제가 없는지 확인한다

3. 시간, 중력, 작동 압력 설정

• 시간 선택 : Steady/Transient
• 중력 벡터 입력
• 작동 압력(Operating Pressure) 입력

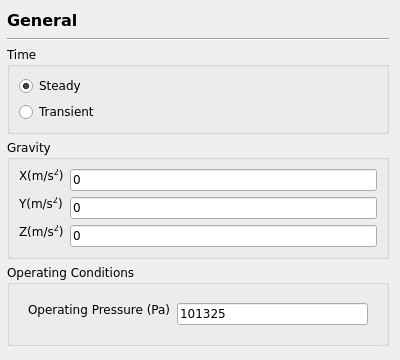
3.1 시간

시간에 따라 유동장이 변하지 않는 문제라면 정상상태를 선택한다. 일부 다상유동 문제에서 시간에 따라 값이 변하지만 특정 시간 이상에서는 값이 변하지 않는 경우 정상상태를 선택한다. 이 경우 LTS(Local Time Step) 기법을 사용한다.

물체가 움직이거나 시간에 따라 조건이 변하는 문제 혹은 고 받음각 유동이나 와류 진동과 같이 유동장이 주기적으로 계속 변하는 조건이라면 비정상상태로 계산해야 한다.

3.2 중력

자연대류 열전달을 고려해야 하는 경우 중력의 방향과 크기를 벡터로 입력한다. 밀도가 다른 여러 개의 상(phase)이 있는 다상유동 문제와 밀도가 다른 여러 화학종이 있는 경우에도 중력을 설정해야 한다.

* 자연대류 고려 여부에 대한 판단 자세히 보기

중력에 의한 자연대류를 포함할지를 결정한다. 자연대류와 강제대류가 차지하는 비중을 판단할 때 부력과 점성력의 비율인 Grashof number, $Gr$와  $Gr/Re^2$ 으로 정의 되는 Richardson number, $Ri$를 사용한다. $Ri$가 1보다 아주 크면 자연대류가 지배적이고 반대이면 강제대류가 지배적이다. 1 근처이면 두 가지를 모두 고려해 주어야 한다. 0,1보다 작으면 자연대류를 무시해도 된다.

$Gr=\frac{\beta\Delta TL^3g}{\nu^2}$

​$\beta$ : thermal expansion coefficient
$L$ : distance
$\nu$ : kinematic viscosity

$Ri = \frac{g \beta (T_{hot} – T_{ref}) L}{V^2}$

$V$ : characteristic velocity

3.3 작동 압력(Operating Pressure)

baramFlow에서 사용하는 모든 압력은 이 값을 기준으로 한 상대 압력이다. 이 값이 0이 되면 모든 압력은 절대 압력을 사용하게 된다.

4. 모델 설정 – 난류, 에너지, 화학종, 사용자 정의 스칼라(passive scalar)

• 난류 모델 선택
• 에너지 방정식 계산 여부 선택
• 화학종 혼합 계산 여부 선택
• 사용자 정의 스칼라 계산 여부 선택

4.1 난류

Inviscid, Laminar, Spalart-Allmaras, k-epsilon, k-omega, DES, LES 를 선택할 수 있다. Inviscid는 점성의 영향을 무시하는 방법으로 고속 압축성 유동에서 일부 사용된다. Laminar는 층류인 경우이며 나머지는 난류 모델로 문제에 따라 적합한 모델을 선택한다.

* 층류화 난류의 판단 방법 자세히 보기

층류인지 난류인지의 판단은 관성력과 점성력의 비율인 Reynolds number($Re$)를 사용하지만, 자연대류 문제에서는 확산과 대류에 의한 열전달 비율인 Rayleigh number($Ra$)를 사용한다.

$Re = \frac{\rho U L}{\mu}$

$L$ : characteristic length
$\mu$ : viscosity

$Ra = \frac{\rho \beta \Delta T L^3 g}{\mu \alpha}$

$\beta$: thermal expansion coefficient(equal to approximately 1/T for ideal gas)
$L$ : distance
$\alpha$: thermal diffusivity

Reynolds number를 이용한 층류/난류 판별 기준은 유동 형태에 따라 다르다. 관내 유동의 경우 Re가 2000보다 작으면 층류 4000보다 크면 난류로 볼 수 있다. 평판 유동에서는 1e05~1e06 정도가 기준이 된다. 개수로 유동의 경우 500 이하이면 층류로 본다.

자연대류 유동에서는 수직 평판 문제일 때 Ra > 1e9 이면 난류로 본다.

* 난류 모델에 대해 자세히 보기

유동이 난류 영역일 때 적절한 난류 모델을 결정한다. RANS(Reynolds-Averaged Navier-Stokes) 모델은 난류의 평균적인 거동을 계산하는 것으로 계산 비용이 낮지만 난류 구조의 세부적인 정보는 소실된다. LES(Large Eddy Simulation)과 DES(Detached Eddy Simulation)은 큰 와류는 직접 계산하고 작은 와류는 모델링하는 방법으로 높은 정확도를 얻을 수 있지만 계산 비용이 매우 높다.

해석을 통해 얻고자 하는 결과에 따라 적절한 모델을 선택해야 한다. 많은 문제들이 RANS 모델로 충분하지만 유동의 박리, 재부착, 천이 등을 정확히 포착해야 하거나 유체 유발 소음(Aero-Acoustics)을 분석하는 경우 LES나 DES가 필요하다.

• Spalart-Allmaras : 항공기 외부 유동과 같이 경계층 유동이 지배적인 문제를 위한 모델로 수정 난류 점성(Modified turbulent viscosity, $\tilde{\nu}$)이라는 하나의 스칼라 방정식을 계산한다.
• k-epsilon : 등방성 난류에 대한 경험식을 이용한 모델로, 난류 운동에너지($k$)와 난류 소산율($\epsilon$) 두 개의 방정식을 계산한다. Standard, RNG, Realizable 모델 등이 있다.
• SST k-omega : 난류 운동에너지($k$)와 난류 비소산율($\omega$) 두 개의 방정식을 계산하는 모델로, 경계층 해석에 적합한 $k-\omega$ 모델과 자유류 해석에 적합한 $k-\epsilon$ 모델을 결합한 것으로 외부 유동 해석에 많이 사용된다.
• LES : 큰 와류는 직접 계산하고 작은 와류는 모델링(3차원, 비정상상태 계산에서만 사용 가능)
• DES : 벽 근처 경계층 유동은 RANS로 처리하고, 와류가 큰 자유 유동 영역은 LES로 처리한다. 3차원, 비정상상태 계산에서만 사용할 수 있다.

4.2 에너지

밀도 기반 솔버를 선택한 경우와 multi-region 격자를 읽어 온 경우 에너지는 자동으로 포함된다.

현재 Baram에서는 다상 유동일 때 에너지 방정식은 포함되지 않는다.

4.3 화학종 혼합

유체가 여러가지 화학종으로 구성되어 있지만 화학종들 간의 물성값 차이가 전체 유동에 미치는 영향이 작을 때는 하나의 화학종으로 처리할 수 있다. 이런 경우 화학종의 분포를 가시화하고 싶을 때는 passive scalar를 이용할 수 있다. 화학종들의 물성값 차이의 영향이 클 때는 각 화학종들의 전달방정식을 계산해야 한다.(현재 Baram에서는 화학반응은 지원하지 않는다.)

* 화학종 계산 방법 자세히 보기

화학종의 diffusion flux 는 다음 식으로 계산된다.

$\vec{J_i}=\ -\left(\rho D_i+\frac{\mu_t}{Sc_t}\right)\nabla Y_i\ =\ -\rho\left(D_i+K\right)\nabla Y_i$

운동량 확산과 질량 확산의 비는 Schmidt number, $Sc$ 인데, 난류가 강할 때 혼합은 난류의 영향이 상대적으로 강해서 분자 확산의 영향은 거의 없기 때문에 turbulent Schmidt number, $Sc_t$를 이용해서 혼합을 계산한다.

$Sc=\frac{\nu}{D}=\frac{viscous \, diffusion \, rate}{molecular \, diffusion \, rate}$

$Sc_t=\frac{\nu_t}{K}$

$K$ : eddy diffusivity $m^2 /s$

turbulent viscosity는 난류 모델에서 계산되며, 주어진 $Sc_t$를 이용해서 eddy diffusivity를 구할 수 있다. $Sc_t$ 값이 작으면 혼합이 더 잘 일어나게 된다.

4.4 사용자 정의 스칼라

다음 식과 같은 임의의 스칼라 방정식을 추가하여 계산할 수 있다. 각 스칼라의 diffusivity를 설정한다.

$\frac{\partial (\rho \phi)}{\partial t} + \nabla \cdot (\rho U \phi)=\nabla \cdot (\Gamma \nabla \phi)+S_{\phi}$

$\Gamma$ : Diffusion coefficient
$S_{\phi}$ : Source term

5. 물성값 설정

• 작동 유체 선택
• 다상 유동과 화학종 혼합 문제일 때 필요한 물질 추가
• 각 물질에 대한 점성계수, 밀도, 정압비열, 열전도도, 분자량 등의 물성값 계산 방법 선택

5.1 점성계수(Viscosity)

유동에 의해 발생하는 전단 응력(shear stress)과 속도의 변화율의 관계가 점성계수이다. 이 관계가 선형인 경우가 Newtonian 유체이며 기울기가 점성계수이다. 이 점성계수는 상수 혹은 온도의 함수로 나타낼 수 있는데 액체의 점성계수는 온도가 올라가면 급속히 감소하고, 기체의 점성계수는 온도가 올라가면 증가한다. 

* 점성계수를 온도의 함수로 나타내는 방법 자세히 보기

온도의 함수로 표현할 때는 Sutherland 관계식이나 polynomial을 사용할 수 있다.

Sutherland 관계식은 기체에만 사용할 수 있으며, 이상기체의 점도를 온도의 함수로 표현한 것으로 Sutherland temperature(Ts)와 Sutherland coefficient(As)로 표현한다.

$\mu=\mu_{ref}\left(\frac{T}{T_{ref}}\right)^{\frac{2}{3}}\frac{T_{ref}+T_s}{T+T_s}=\frac{A_sT^{\frac{2}{3}}}{T+T_s}$

공기의 경우 $T_{ref}$ =273.15K 일 때 $\mu_{ref}$ =1.716e-5 kg/ms, $Ts$=110.4K, $As$=1.458e-6

유동에 의해 발생하는 전단 응력(shear stress)과 속도의 변화율이 선형이 아닌 경우는 non-Newtonian 유체이다. 이 때 점성계수를 정의하는 방법으로 power law, cross power law, Herschel-Bulkley, Bird-Carreau 모델 등이 있다.

물체에 힘을 가했을 때 탄성 변형과 점성을 지닌 흐름이 동시에 나타나는 점탄성(viscoelasticity) 문제는 현재 Baram에서는 지원하지 않는다.

5.2 밀도(Density)

밀도를 정의하는 방법은 상수, constant, perfect gas, polynomial, incompressible perfect gas 등을 선택할 수 있다.

* 밀도 계산 방법 자세히 보기

Perfect gas

Perfect gas와 Ideal gas는 기체 입자간의 상호작용(inter-molecular forces)을 무시할 수 있어 이상기체 상태방정식($p=\rho RT$)을 만족하는 기체이다. 일반적으로 두 용어는 같은 의미로 쓰이는데 사람에 따라 perfect gas는 열용량(heat capacity, $C_p$와 $C_v$)이 상수인 경우를, ideal gas는 열용량이 상수이거나 온도만의 함수인 경우를 말하기도 한다. Cp가 상수인 경우를 calorically perfect gas(열량적 완전기체), 온도의 함수인 경우를 thermally perfect gas(열적 완전기체)로 구분하기도 한다.

Polynomial

온도에 대한 함수로 다음의 식으로 계산한다.

$S = a_0 \cdot T^0 + a_1 \cdot T^1 + a_2 \cdot T^2 + … + a_n \cdot T^n$

Incompressible perfect gas

밀도를 온도만의 함수로 표현하는 방법이다. 압력 변화의 영향은 무시하는데 이상기체 상태방정식에서 압력은 주어진 상수 값을 사용한다. 압력의 변화가 크지 않고 온도 변화가 큰 문제나 대기경계층 문제 등에 사용할 수 있다.

$p_{op\ }=\rho RT$

$p_{op}$ : reference pressure

이 외에 Boussinesq approximation, Perfect fluid, Real gas, Linear 모델 등이 있는데 아직 Baram에서는 지원하지 않는다.

5.3 비열(Heat capacity)

상수 혹은 온도에 대한 polynomial 함수로 정의할 수 있다.

* Perfect gas일 때 비열 계산 방법 자세히 보기

perfect gas일 때 $C_p$, $C_v$는 다음의 식으로 나타낼 수 있다.

$C_p-C_v=R$

$\gamma=\frac{C_p}{C_v}$

$C_p=\frac{\gamma R}{\gamma-1}$

$R$ : 기체상수
$\gamma$ : 비열비

5.4 열전도도(Thermal conductivity)

열전도도는 상수 혹은 온도의 함수를 사용할 수 있다. 온도의 함수일 때 polynomial과 Chapman-Enskog approximation를 사용할 수 있다.

점성계수를 Sutherland 식을 사용할 때 열전도도 역시 Chapman-Enskog approximation을 사용하여 다음과 같이 계산한다.

$\kappa=\mu C_v\left(1.32+1.77\ \frac{R}{C_v}\right)$

6. Cell zone 조건 설정

• 다중 영역 문제일 때 각 영역의 물질 선택
• 다상 유동일 때 각 상(phase)의 물질 선택
• 캐비테이션 계산 여부와 모델 선택
• Cell zone type 선택 – None, Multiple Reference Frame, Porous Zone, Sliding Mesh, Actuator Disk
• Source Term 설정
• Fixed Value 조건 설정

6.1 Porous media

다공성 물질이나 작은 영역에 매우 복잡한 형상이 있을 때, 형상을 직접 구현하지 않고 유속에 따른 압력 손실로 모델링하는 방법이다. 압력 손실의 모델링 방법으로 Darcy-Forchheimer 모델과 Power law 모델을 사용할 수 있다.

* Porous media 모델 자세히 보기

Porous media 모델은 Darcy Forchheimer와 Power law 두 가지가 있다.

Darcy-Forchheimer

3가지 방향에 대한 압력 손실을 각각 설정할 수 있다. 방향은 두 개의 벡터에 의해 결정된다. 두 벡터는 입력값(Direction-1 Vector, Direction-2 Vector)에 의해 결정되고 세번째 방향은 두 벡터에 수직한 방향이다.

관성 저항 계수(Inertial Resistance Coefficient(f, Forchheimer coefficient))와 점성 저항 계수(Viscous Resistance Coefficient(d, Darcy coefficient))를 벡터로 입력한다. 압력손실은 다음 식으로 계산한다.

$S_i=-\left(\mu d_i\ +\ \frac{1}{2}\rho\left|U\right|f_i\right)U_i$

$d$ : Darcy coefficient $[1/m^2]$, vector
$f$ : Forchheimer coefficient $[1/m]$, vector

Power law

$C_0$, $C_1$ 두 개의 계수를 이용해 다음 식으로 계산한다.

$S=-\rho C_0\left|U\right|^{\left(C_1-1\right)}U$

$C_0$ : linear coefficient, empirical coefficient
$C_1$ : expansion coefficient, empirical coefficient

6.2 MRF(Multiple Reference Frame)

회전하는 물체를 시뮬레이션 할 때 물체를 회전시키지 않고 회전체 주변의 유동을 회전상대좌표계에서 계산하는 방법이다. 정상상태 계산을 할 수 있기 때문에 계산 비용이 상대적으로 낮다는 장점이 있다.

* MRF 설정 항목 자세히 보기

• 회전속도(Rotating Speed) : 분당 회전수(RPM, Revolution Per Minute)
• 회전축 중심 좌표(Rotating Axis Origin)
• 회전축 방향(Rotating Axis Direction) : textcolor[rgb]{0.6,0,0}{오른손 법칙에 따라 회전 방향이 반시계 방향이 되도록 설정}
• 셀존 안의 움직이지 않는 경계면(Static Boundary) : textcolor[rgb]{0.6,0,0}{인터페이스 면도 선택해야 한다}. 2개의 인터페이스 면 중 어느 것이 해당 셀존에 있는 것인지 알기 어려울 때는 모두 선택하면 된다. 셀존에 있지 않는 면이 포함되더라도 계산에 영향을 미치지 않는다.

6.3 Sliding Mesh

Sliding mesh는 운동하는 물체 주위를 셀존으로 구성하고 격자를 움직이는 방법이다. 운동하는 셀존과 정지한 셀존의 각 경계면은 인터페이스로 구성해야 한다. 셀존 내부에 있는 움직이는 경계면은 움직이는 벽(moving wall) 경계조건을 사용해햐 한다. 설정 항목은 회전속도(RPM), 회전축 중심 좌표, 회전 방향이며 회전 방향은 MRF에서와 같다.

6.4 Actuator disk

액추에이터 디스크 모델은 프로펠러와 같은 회전체의 복잡한 형상을 모델링하지 않고 디스크로 모델링하여 평균적인 속도의 생성항으로 처리한다. Froude와 variable-scaling 두 가지 방법이 있다.

* Froud이 Variable-scaling 방법 자세히 보기

Froude’s method

$T\ =\ 2\rho_{ref}A\left|u_m\cdot n\right|^2a\left(1-a\right)$

$T$ : Thrust magnitude $[N]$
$⍴_ref$ : Monitored incoming fluid density $[kg/m^3]$
$A$ : Actuator disk planar surface area $[m^2]$
$u_m$ : incoming velocity spatial-averaged on monitored region $[m/s]$
$n$ : surface normal vector of the actuator disk pointing upstream [-]
$a$ : Axial induction factor [-]

$a=1-\frac{C_p}{C_T}$

$C_p$ : power coefficient [-]
$C_T$ : Thrust coefficient [-]

Variable-scaling method

$T\ =\ 0.5\rho_{ref}A\left|u_0\cdot n\right|^2C_T^{\ast}$

$u_0$ : incoming velocity spatial-averaged on actuator disk $[m/s]$

${C_T}^*$ : Calibrated thrust coefficient [-]

${C_T}^* = C_T \left ( \frac{|u_m|}{|u_0|} \right )^2$

6.5 Source Terms

에너지, 질량, 난류 관련 필드 등에 생성항을 줄 수 있다. 생성항의 크기를 주는 방법은 ‘전체 체적에 대한 값'(Value for Entire Cell Zone)과 ‘단위 체적당 값'(Value per Unit Volume)을 주는 두 가지가 있다.

비정상상태 문제일 때 생성항을 시간에 따라 변하는 값으로 줄 수 있는데, 조각별 선형함수(piecewise linear)와 다항식(polynomial) 방법이 제공된다.

6.6 Fixed Value 

셀존의 속도 벡터, 온도, 난류 등의 평균값을 고정할 수 있다. 속도의 경우 계산의 불안정성이 발생할 수 있어 완화계수(relaxation factor)를 사용한다.

7. 경계조건 설정

• 입구 조건 설정
• 출구 조건 설정
• 벽면 조건 설정
• Interface 조건 설정

* 경계조건의 종류 자세히 보기

입구의 유동 경계조건

• Velocity Inlet: 속도 성분 혹은 면에 수직 방향의 크기를 줄 수 있다.
• Pressure Inlet: 전압력(total pressure)를 줄 수 있다.
• Flowrate Inlet : 질량유량 혹은 체적 유량을 줄 수 있다.
• Atmospheric boundary layer Inlet: 지표면 조건과 기준 높이에서의 속도를 줄 수 있다.
• Open channel inlet : 자유수면을 계산할 때 입구에 일정한 유량을 주고 그에 따라 수면의 높이가 변할 수 있는 조건이다.
• Freestream : 비압축성 외부 유동 해석을 자유류 조건이다.
• Far-field Riemann : 압축성 유동의 자유류 조건이다.
• Supersonic inlet : 유동의 입구가 초음속인 경우 사용하는 경계조건이다.
• Subsonic inlet : 압축성 유동에서 유체기계와 같은 내부유동의 입구 아음속 경계조건이다.

출구의 유동 경계조건

• Pressure outlet : 출구 경계면에 일정한 압력을 주는 조건이다. 입력한 압력은 유동이 빠져나가는 경우는 정압(static pressure)로, 들어오는 경우는 전압력(total pressure)로 사용된다. 압력을 입력하고 유동이 유입될 때의 조건과 ‘Non-Reflecting Boundary’를 옵션으로 선택할 수 있다.
• Outflow : 출구의 모든 필드에 대해 구배(gradient)가 0인 조건을 사용한다.
• Open channel outlet : 자유수면을 계산할 때 출구에 일정한 평균 속도를 주고 그에 따라 수면의 높이가 변할 수 있는 조건이다.
• Supersonic outlet : 압축성 유동에서 유체기계와 같은 내부유동의 출구 아음속 경계조건이다.
• Subsonic outlet : 압축성 유동의 출구속도가 초음속일 때 사용하는 경계조건이다.

벽면의 유동 경계조건

• No-slip : 벽면에서 속도가 0인 조건
• Slip : 마찰이 없는 벽면, 벽면에 수직한 속도 성분이 0인 조건
• Atmospheric wall : 대기경계층의 지표면
• Moving wall : 특정한 속도를 지정
• Wall roughness : 표면 거칠기를 이용하여 난류 점성계수를 계산

벽면의 온도 경계조건

• Adiabatic : 열의 유입/유출이 없는 단열 조건
• Constant temperature : 일정한 온도 조건
• Constant heat flux : 일정한 열유속 조건
• Convection and Radiation : 경계면에서 외부로 대류 및 복사 열전달이 있는 조건
• Solid layer : 여러 물질의 고체 층이 있는 경우 열전도를 1차원으로 계산

interface 조건

• Thermo-coupled wall : 계산 영역 내부의 두께가 없는 벽면
• Internal interface : 계산 영역 내부의 두께가 없고 유동이 통과하는 경계면
• Rotational periodic : 회전 주기 조건
• Translational periodic : 병진 주기 조건
• Region interface : 다중 영역 문제에서 region 간의 경계
• Porous jump : 두께가 없는 면에서 압력 변화 조건
• Fan : 두께가 없는 면에서 속도-압력 관계를 주는 조건

8. 수치해석 기법 설정

• pressure-velocity coupling 선택 : SIMPLE 혹은 SIMPLEC를 선택. SIMPLEC를 선택하고 완화계수를 0.9 이상의 값을 주면 수렴 속도가 빨라질 수 있으나 안정성에 문제가 있을 수 있다
• 이산화(Discretization) 기법 설정 : 시간, 압력, 운동량, 에너지, 난류, vof, 화학종, 스칼라 등에 대한 이산화 기법을 설정한다.
• 수렴 판정 조건(Convergence criteria)을 설정한다.
• 완화계수(relaxation factors)를 설정한다.
• 비정상상태일 때 계산 조건을 설정한다 – 시간당 반복계산 회수(Max Iterations per Time Step), 압력보정 회수(Number of Correctors)
• 에너지방정식의 viscous dissipation, kinetic energy, pressure work 포함 여부 결정

* 에너지방정식의 항목 선택 방법 자세히 보기

점성가열(Viscous dissipation term)

점성력에 의해 기계적 에너지가 열에너지로 변환되는 현상으로 대부분의 경우 무시할 수 있지만, 고속 유동이나 점성이 매우 큰 윤활 유동 등에서는 무시할 수 없다. 점성 가열의 중요도 평가는 소산된 에너지와 전도된 에너지의 비율인 Brinkman number, $Br$ 를 사용할 수 있다.

$Br =Ec \cdot Pr = \frac{U^2 \mu}{k \Delta T}$

$Ec$ : Eckert number

$\mu$ : viscosity

$k$ : conductivity

$Br$이 1보다 매우 작으면 점성 가열은 무시할 수 있다.

운동에너지(Kinetic Energy)

운동에너지가 열에너지로 변환되는 현상에 대한 항이다. 비압축성 유동에서는 무시할 수 있으나, 고속 압축성 유동과 고온 가스 유동일 때 무시할 수 없다. 운동에너지와 열에너지의 상대적 크기를 비교하는 Eckert number, $Ec$를 이용해서 중요도를 평가할 수 있다.

$Ec = \frac{U^2}{C_p \Delta T}$

$C_p$ : heat capacity

$E_c$가 1보다 매우 작으면 운동에서지 항은 무시할 수 있다.

압력 일(Pressure Work)

유체가 압축되거나 팽창할 때의 일을 의미하며 펌프, 터빈, 압축기 등의 문제와 고속 압축성 유동에서 중요한 항목이 된다.

9. 모니터링 설정

정상상태 문제에서 수렴성 확인을 위해, 비정상상태 문제에서는 시간에 대한 값의 변화를 확인하기 위해, 힘, 평균, 적분, 최대값, 최소값, 유량 등의 모니터링을 설정한다.

• Force : 면에 작용하는 힘과 유체력 계수(Cd, Cl, Cm)
• Point : 특정 좌표에서 유동 변수의 값을 모니터링
• Surface : 특정 면에서 유량, 유동변수의 평균, 적분, 최대값, 최소값, 변동률(CoV)를 모니터링
• Volume :특정 영역에서 유량, 유동변수의 평균, 적분, 최대값, 최소값, 변동률(CoV)를 모니터링

10. 초기화 및 계산

• 모든 유동 변수에 대한 초기조건을 설정
• 공간의 특정 영역에 일정한 값을 설정
• 계산 조건 설정
  • Number of Iteration, End Time : 정상상태일 때 반복계산 회수와 비정상상태일 때 종료 시간
  • Time Step Size : 비정상상태일 때 시간 전진 간격
  • Time Stepping Method : 비정상상태일 때 시간 전진 방법. Fixed 혹은 Adjust Time Step
  • Auto Save Interval : 자동 저장 간격
  • Max CFL Number : Adjust Time Step 방법을 사용할 때 최대 CFL number

* Adjust Time Step과 CFL Number 자세히 보기

CFL number는 Courant number라고도 하는데, 속도와 계산 격자의 간격을 고려해 시간 간격을 얼마로 설정해야 하는지를 나타낸다. 1 이하의 값이어야 안정적이고 정확한 답을 얻을 수 있으나 계산 시간을 줄이기 위해 1보다 큰 값을 사용할 수도 있다. Adjust time step은 주어진 Max CFL number를 이용해서 아래의 식을 이용해 시간 간격을 결정한다.

$C = \frac{v \Delta t}{\Delta x}$

밀도 기반 압축성 솔버일 때 CFL number는 이와 다르게 Pseudo time에 대한 값으로 실제 시간과는 무관한 수치 수렴을 위한 시간 변수이다.